地球の外周は4万kmです

なぜ地球の外周はピッタリ4万kmなのか

地球の外周はちょうど4万kmですが、どうしてこんなにピッタリの数字になったのか、その理由を知っていますか。

身も蓋もない話なのですが、実は、誰かがそう決めたからなんです。

1791年にフランスの科学アカデミーが地球の子午線全周長を4千万分の1にした長さを1メートルと決めたのです。

つまり、地球の外周は4万kmにしようよって。

そんなこと言っても、地球は回転体だから遠心力で赤道付近が太くなり、必然的に楕円形になるから不正確だろう。

確かに、赤道部分の半径は、北極、南極部分の半径よりも21kmも長いのです。

しかも、標高8000mのヒマラヤ山脈や、死海のような海抜マイナス400mの凹地があるから、表面は平滑でないし長さが不正確になるだろうって。

そんな風に思ってしまいますよね。
たしかにそういう懸念もあります。

でも大丈夫です。

卵の殻の厚さは0.3mmほどですが、上に述べたような誤差要因は、すべて卵の殻ほどの極めて薄い膜の中の出来事なのです。

みなさんに、0.3mmの細芯シャープペンシルで正確に直径10cmの円を書いていただきましょう。
きれいな円が描けたでしょうか。

そうすると驚いたことに、0.3mmの線幅は、地球の大きさでは38kmの長さに相当するのです。

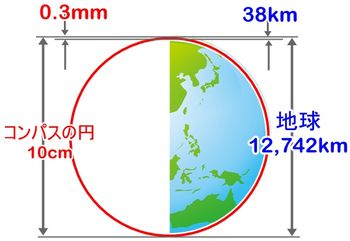
大気中の対流圏が地表から10km程までですから、台風も暴風雪も地表の擾乱はすべて、わずか0.3mmの細線の幅内での出来事になります。

634mの東京スカイツリーも、8848mのエベレストも、飛行機が飛ぶ高さも、0.3mmの線幅内に収まってしまいます。

また、楕円形の要因となっている、極地方と赤道との半径差21kmも線幅の範囲内の誤差です。

つまり、地球は真円で表面は平滑だとみなしても、実質的には問題がありません。

しかし、科学技術の進歩に連れて厳密に議論するといろいろと問題があるので、現在では、メートルの長さが厳密に定められて、真空中の光の速度を基準に定義されています。

さて、どうしてこんな話をしているかというと、気象予報士の試験問題では、天気図上の距離を求める問題がしばしば出題されています。

典型的なのは、台風や低気圧の移動距離や、移動速度を求める問題です。
例えば、こんな問題です。

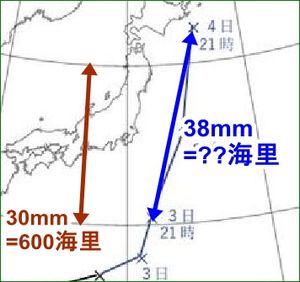
ここで距離を示すスケールが与えられていれば悩む必要はありませんが、距離を示すデータが何も与えられていない場合は、上図のように天気図内の情報から読み取ることになります。

天気図には必ず緯線と経線が与えれていますね。

この緯線が距離を示す情報なのです。

緯線間10°例えば北緯30～40°の距離が1111kmになります。
どうしてそうなるか理屈を覚えておきましょうね。

地球を輪切りにした断面を、時計の文字盤にみなして考えます。

12時＝北極（北緯90°）
3時＝赤道（北緯0°）

さらに
1時＝北緯60°
2時＝北緯30°

12時から3時までの外周が、地球の外周4万kmの4分の1なので1万kmになりますね。

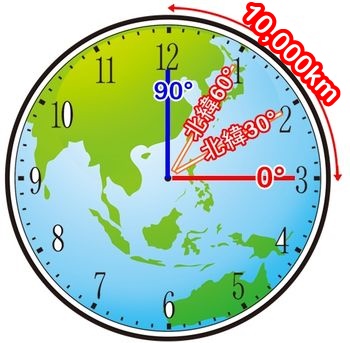
赤道から北極までが1万kmで、これを90分割したのが緯度ですから、

1°の長さ＝10,000km/90°＝111kmとなるのです。
北緯20°~北緯30°のような10°間の距離は、1111kmですね。

天気図では、北緯30°～北緯40°の距離を読み取る問題が多いのですが、この距離が1111kmであることは、その理屈を含めて覚えておくと、いざというときにうっかり忘れていても、思い出すことが出来ます。

【10,000kmを90で割ると、1°の距離になる】

また、答えを海里で求める問題や、速度をノットで求める問題では『海里』を使います。

1海里は1/60度＝1分の距離なので、
1海里＝111km/60=1.852km（一箱に）となるのです。

語呂合わせ呪文
『海里は一箱に詰めてヨットで来いよ』も見ておいてください。

このように、基準になる距離が一つ分かれば、問題の距離が計算できますね。
計算ミスをしないように気をつけてください。